Tačke u dvodimenzionalnom prostoru

Autor zadatka: Rade Radišić <radisic.rade@uns.ac.rs>

Tačke u dvodimenzionalnom Dekartovom koordinatnom sistemu opisane su preko njihovih koordinata:

  • Vrednost na x-osi (realan broj dvostruke preciznosti)

  • Vrednost na y-osi (realan broj dvostruke preciznosti)

Učitati tačke iz ulazne datoteke, potom uraditi sledeće:

  1. Pronaći koordinate težišne tačke za niz učitanih tačaka. Za pronalaženje koordinata težišne tačke potrebno je naći posebno aritmetičku sredinu x i y koordinata tačaka čija se težišna tačka nalazi (formula je na drugoj stranici dokumenta).

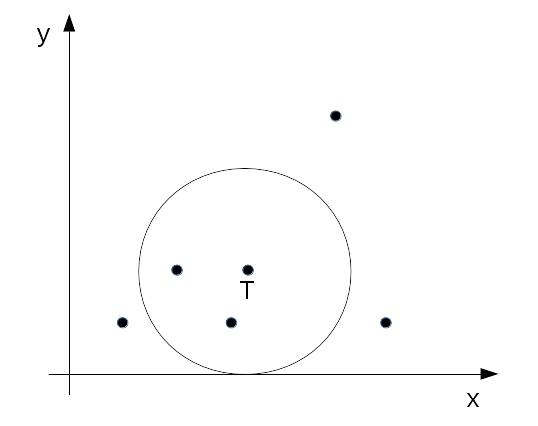
  2. Pronaći sve tačke koje pripadaju krugu sa centrom u težišnoj tački (rezultat prethodnog koraka) i poluprečnika koji se unosi kao argument komandne linije (može biti realna vrednost). Rezultat ovog i prethodnog koraka upisati u izlaznu datoteku čiji se naziv sastoji od stringa pripada_krugu_poluprecnika_, vrednost poluprečnika (argument komandne linije) i ekstenzijom .txt.

  3. Pronaći ukupan broj jedinstvenih trouglova koji može da nastane od datog niza tačaka. Da bi neke tri tačke sačinjavale trougao, potrebno je da duži koje one međusobno grade zadovoljavaju nejednakost trougla (formula je na drugoj stranici dokumenta). Dobijeni broj trouglova upisati u izlaznu datoteku "trouglovi.txt".

../../../../_images/tacke2d_ilustracija.png

Primer poziva programa:

./a.out tacke.txt 5

Primer ulazne datoteke tacke.txt:

1 1
2 2
3 1
5 5
6 1

Primer izlazne datoteke trouglovi.txt:

Broj trouglova: 8

Primer izlazne datoteke pripada_krugu_poluprecnika_2.txt

Krug poluprecnika 2.00 sa centrom u tacki (3.40, 2.00)

(2.00, 2.00)
(3.00, 1.00)

Primer poziva programa gde tačke ne sačinjavaju trougao:

./a.out ne_trougao.txt 5

Primer ulazne datoteke ne_trougao.txt:

1 1
2 2
3 3

Primer izlazne datoteke trouglovi.txt:

Broj trouglova: 0

Primer izlazne datoteke pripada_krugu_poluprecnika_5.txt

Krug poluprecnika 5.00 sa centrom u tacki (2.00, 2.00)

(1.00, 1.00)
(2.00, 2.00)
(3.00, 3.00)

Korisne matematičke formule

Računanje težišne tačke

Koordinate težišne tačke \((x_{T}, y_{T})\) za \(n\) tačaka računaju se na sledeći način:

\[ \begin{align}\begin{aligned}x_{T} = \frac{(x_{1} + x_{2} + ... + x_{n})}{n}\\y_{T} = \frac{(y_{1} + y_{2} + ... + y_{n})}{n}\end{aligned}\end{align} \]

Nejednakost trougla

Za svaki trougao sa stranicama \(a\), \(b\) i \(c\) treba da važe sledeće nejednakosti:

\[ \begin{align}\begin{aligned}a + b > c\\c + b > a\\c + a > b\end{aligned}\end{align} \]

Rastojanje između dve tačke u dvodimenzionalnom koordinatnom sistemu

Date su dve tačke sa koordinatama \((x_{1}, y_{1})\) i \((x_{2}, y_{2})\). Njihovo rastojanje može se odrediti na sledeći način:

\[d = \sqrt{(x_{1} - x_{2})^2 + (y_{1} - y_{2})^2}\]

Primer rešenja

  1#include <stdio.h>
  2#include <string.h>
  3#include <stdlib.h>
  4#include <math.h>
  5
  6#define MAX_SIZE 30
  7#define MAX_NAZIV 41
  8
  9typedef struct tacka_st {
 10    double x;
 11    double y;
 12} TACKA;
 13
 14FILE *safe_fopen(char *, char *, int);
 15void ucitaj_tacke(FILE *, TACKA *, int *);
 16void ispisi_tacke(FILE *, TACKA *, int);
 17void ispisi_tacku(FILE *, TACKA);
 18
 19unsigned prebroj_trouglove(TACKA *, int);
 20TACKA pronadji_teziste(TACKA *, int);
 21void pripada_krugu(TACKA *, TACKA *, 
 22                   int, int *, TACKA, double);
 23
 24int obrazuju_trougao(TACKA, TACKA, TACKA);
 25double udaljenost(TACKA, TACKA);
 26
 27int main(int argc, char **argv) {
 28    TACKA tacke[MAX_SIZE], pripadaju_krugu[MAX_SIZE];
 29    int n, m;
 30
 31    if(argc != 3) {
 32        printf("Niste dobro pozvali program. Primer poziva: %s tacke.txt 5\n", argv[0]);
 33        exit(EXIT_FAILURE);
 34    }
 35
 36    FILE *pin = safe_fopen(argv[1], "r", EXIT_FAILURE);
 37    ucitaj_tacke(pin, tacke, &n);
 38    fclose(pin);
 39
 40    // a)
 41
 42    char naziv[MAX_NAZIV];
 43    strcpy(naziv, "pripada_krugu_poluprecnika_");
 44    strcat(naziv, argv[2]);
 45    strcat(naziv, ".txt");
 46
 47    double r = atof(argv[2]);
 48    TACKA teziste = pronadji_teziste(tacke, n);
 49
 50    FILE *pout = safe_fopen(naziv, "w", EXIT_FAILURE);
 51    fprintf(pout, "Krug poluprecnika %.2lf sa centrom u tacki ", r);
 52    ispisi_tacku(pout, teziste);
 53    fprintf(pout, "\n");
 54
 55    // b)
 56
 57    pripada_krugu(pripadaju_krugu, tacke, n, &m, teziste, r);
 58    ispisi_tacke(pout, pripadaju_krugu, m);
 59
 60    fclose(pout);
 61
 62    // c)
 63
 64    pout = safe_fopen("trouglovi.txt", "w", EXIT_FAILURE);
 65    fprintf(pout, "Broj trouglova: %u\n", prebroj_trouglove(tacke, n));
 66
 67    fclose(pout);
 68
 69    return EXIT_SUCCESS;
 70}
 71
 72FILE *safe_fopen(char *pname, char *pmode, int error_code) {
 73    FILE *pf = fopen(pname, pmode);
 74
 75    if(pf == NULL) {
 76        printf("Datoteka sa imenom %s nije uspesno otvorena.\n", pname);
 77        exit(error_code);
 78    }
 79
 80    return pf;
 81}
 82
 83void ucitaj_tacke(FILE *pin, TACKA *tacke, int *pn) {
 84    int i = 0;
 85
 86    while(fscanf(pin, "%lf %lf", &tacke[i].x,
 87                                 &tacke[i].y) != EOF) {
 88        i++;
 89    }
 90
 91    *pn = i;
 92}
 93
 94void ispisi_tacke(FILE *pout, TACKA *tacke, int n) {
 95    int i;
 96
 97    for(i = 0;i < n;i++) {
 98        ispisi_tacku(pout, tacke[i]); 
 99    }
100}
101
102void ispisi_tacku(FILE *pout, TACKA tacka) {
103    fprintf(pout, "(%.2lf, %.2lf)\n", tacka.x, tacka.y);
104}
105
106unsigned prebroj_trouglove(TACKA *tacke, int n) {
107    int i, j, k;
108    unsigned broj_trouglova = 0;
109
110    for(i = 0;i < n;i++) {
111        for(j = i + 1;j < n;j++) {
112            for(k = j + 1;k < n;k++) {
113                if(obrazuju_trougao(tacke[i],
114                                    tacke[j],
115                                    tacke[k])) {
116                    broj_trouglova++;
117                }            
118            }
119        }
120    }
121
122    return broj_trouglova;
123}
124
125TACKA pronadji_teziste(TACKA *tacke, int n) {
126    int i;
127    double suma_x = 0, suma_y = 0;
128
129    TACKA tezisna_tacka;
130
131    for(i = 0;i < n;i++) {
132        suma_x += tacke[i].x;
133        suma_y += tacke[i].y;
134    }
135
136    tezisna_tacka.x = suma_x / n;
137    tezisna_tacka.y = suma_y / n;
138
139    return tezisna_tacka;
140}
141
142void pripada_krugu(TACKA *pripada, TACKA *tacke, 
143                   int n, int *pm, TACKA centar, double r) {
144    int i, j = 0;
145
146    for(i = 0;i < n;i++) {
147        if(udaljenost(tacke[i], centar) <= r) {
148            pripada[j] = tacke[i];
149            j++;
150        }
151    }
152
153    *pm = j;
154}
155
156int obrazuju_trougao(TACKA t1, TACKA t2, TACKA t3) {
157    double a = udaljenost(t1, t2);
158    double b = udaljenost(t2, t3);
159    double c = udaljenost(t1, t3);
160
161    return (a + b > c) && (b + c > a) && (c + a > b);
162}
163
164double udaljenost(TACKA t1, TACKA t2) {
165    return sqrt(pow(t1.x - t2.x, 2) + pow(t1.y - t2.y, 2));
166}
167